Bônus: plotagem de gráficos em Python¶

Em uma grande quantidade de aplicações, é desejável visualizar os dados ou resultados de forma gráfica. Para suprir essa necessidade, Python oferece uma biblioteca extremamente flexível para a geração de gráficos de diversos tipos, denominada matplotlib

É possível utilizá-la para gerar gráficos na tela, ou até com a qualidade exigida para publicações impressas, por exemplo.

Para entender como ela funciona, vejamos um exemplo simples: aqui a ideia é apenas desenhar uma linha.

import matplotlib.pyplot as plt
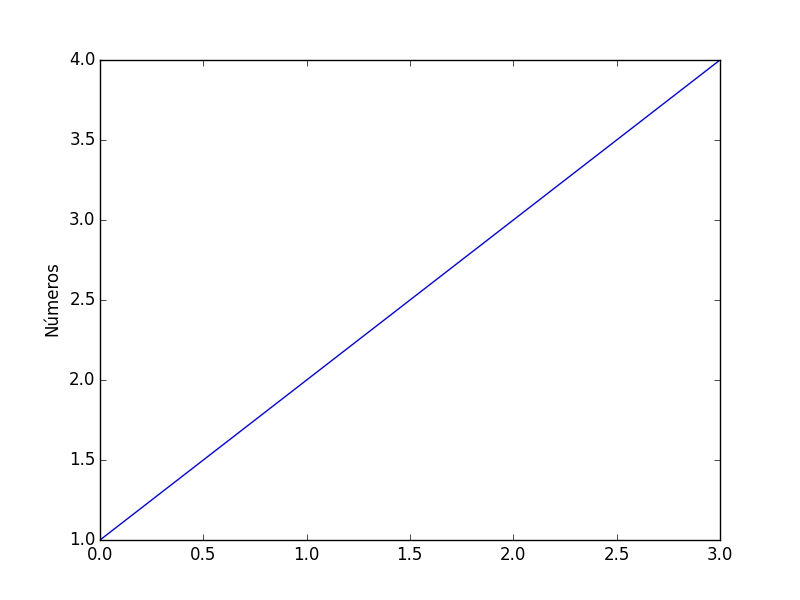
plt.plot([1, 2, 3, 4])
plt.ylabel("Números")
plt.show()

Vamos entender como esse programa funciona:

O primeiro comando importa a biblioteca matplotlib, em particular um módulo denominado pyplot e define que seu nome no programa será plt (apenas por conveniência)
O segundo comando usa o módulo pyplot para gerar um gráfico a partir de uma lista de números. Essa lista especifica as coordenadas y de cada número.
O terceiro comando define um rótulo (ylabel) para o eixo Y do gráfico
Finalmente, o comando plt.show() exibe o gráfico numa nova janela

Nota

Observe que as coordenadas para o eixo X foram geradas automaticamente. Como especificamos 4 coordenadas para Y, Python usa uma sequência de 0 a 3 para o eixo X.

Normalente, é desejável especificar duas sequências: uma para o eixo X e outra para o eixo Y. Para isso, basta enviar duas listas para o comando plot:

import matplotlib.pyplot as plt
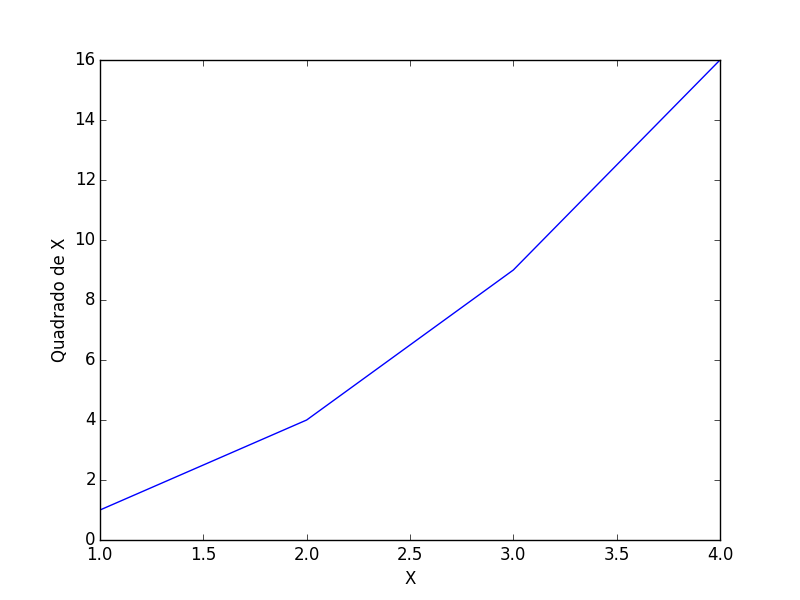
plt.plot([1, 2, 3, 4], [1, 4, 9, 16])
plt.ylabel("Quadrado de X")
plt.xlabel("X")
plt.show()

Obviamente, não é muito prático gerar um gráfico com sequências determinadas, porque é difícil preencher manualmente essas listas.

Dessa forma, uma alternativa possível é usar um comando de repetição (for ou while) para preencher as listas automaticamente.

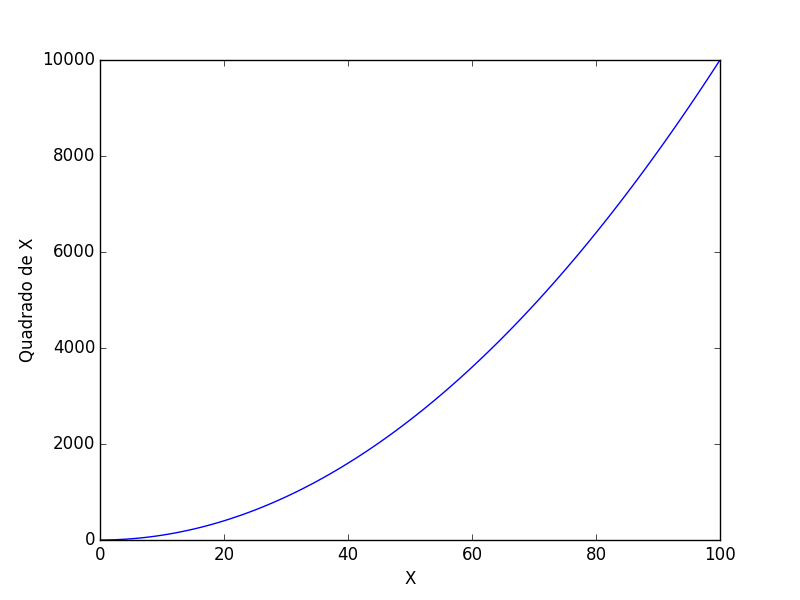
Por exemplo, supondo que desejamos gerar um gráfico com os quadrados de cada número no intervalo (0,100):

import matplotlib.pyplot as plt

# Define duas listas vazias
x = []
y = []

# Preenche as listas
for coordx in range(0,101):
    x.append(coordx)
    y.append(coordx ** 2)

# Desenha o gráfico
plt.plot(x, y)
plt.ylabel("Quadrado de X")
plt.xlabel("X")
plt.show()

Vamos entender esse programa:

x = [] cria uma lista vazia (o mesmo é feito para y)
Na repetição, usamos a função append de cada lista para acrescentar um valor à lista. Dessa forma, no final teremos as duas listas preenchidas com os valores
Finalmente, o comando plt.plot recebe as listas já preenchidas e desenha o gráfico.

É possível controlar completamente a aparência do gráfico, mas para isso pesquise a documentação do pyplot. Por exemplo, se quisermos desenhar pontos ao invés de linhas, fazemos:

...
# Desenha o gráfico
plt.plot(x, y, 'ro')
plt.ylabel("Quadrado de X")
plt.xlabel("X")
plt.show()

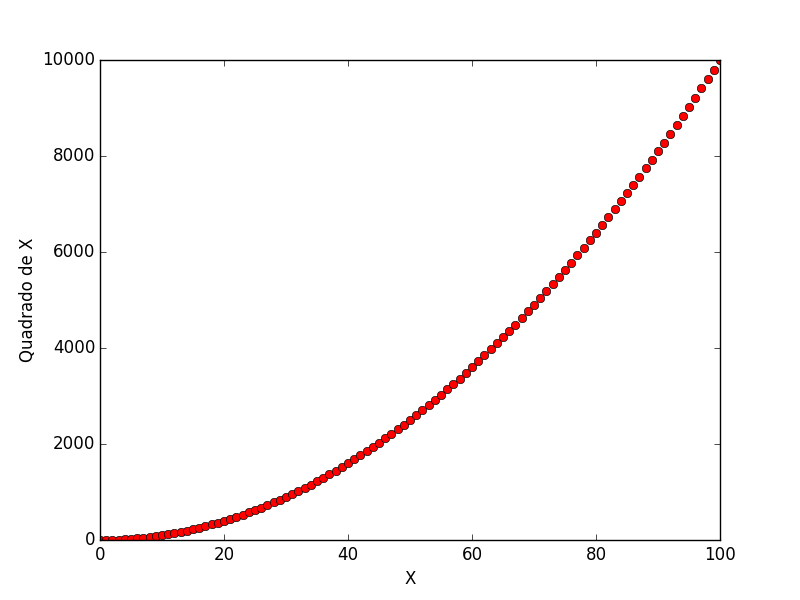
Neste exemplo, veja que o comando plt.plot tem um terceiro argumento: ele especifica a aparência dos pontos - agora eles são vermelhos (r) e desenhados com círculos (o). O padrão, que usamos antes, é b-, ou seja, linhas azuis.

Se você quiser plotar mais de uma sequência ao mesmo tempo, basta usar outro comando plt.plot antes do plt.show.

Exercícios¶

Altere o programa anterior para plotar também o gráfico da função \(3x^2\). Dica: você precisará criar mais uma lista e usar o comando plt.plot mais de uma vez. Veja abaixo como adicionar uma legenda para cada lista de pontos:
```
...
# Desenha o gráfico
plt.plot(x, y, 'ro', label='x2')
plt.plot(x, y2, 'ro', label='3x2') # Supondo que y2 é outra lista...
plt.xlabel("X")
plt.legend() # adiciona a legenda
plt.show()
```

Utilizando como base o exercício de lançamento de projétil, escreva um programa para desenhar o gráfico da distância x altura. Lembre-se que as entradas são as mesmas: velocidade inicial (em km/h), ângulo de lançamento e altura inicial.

import math

g = 9.81

v0 = float(input("Velocidade inicial:"))
ang = float(input("Ângulo:"))
y0 = float(input("Altura inicial:"))

ar = math.radians(ang)

y = y0
x = 0
while y >= 0:
   y = x * math.tan(ar) - 1/(2*v0**2) * g*x**2/math.cos(ar)**2 + y0
   print(x,"\t",y)
   x = x + 0.05

Os números de Fibonacci (ver exercício 4 da lista de while) têm diversas propriedades interessantes. Uma delas é que a divisão de um número pelo anterior (a partir do terceiro) gera sempre o mesmo resultado: uma aproximação de um número conhecido como razão áurea.

Esse número pode ser encontrado em diversos locais, especialmente na Natureza. Por exemplo, essa figura de um girassol mostra a distribuição das sementes, e há uma relação direta do posicionamento delas com a razão áurea. O valor exato pode ser calculado por \(\phi = \frac{1 + \sqrt{5}}{2} \approx 1.6180339887...\):

Na verdade, a relação é em relação ao ângulo através do qual as sementes são “posicionadas” na flor. Para gerar as coordenadas de cada semente, podemos usar o seguinte algoritmo:
- Calcular o “ângulo áureo”: \(360 - \frac{360}{\phi}\)
- Inicializar o ângulo atual com zero (ang)
- Criar duas listas vazias, para x e y
- Repetir usando um contador (quantidade de sementes):
  - Calcular a distância, através da raiz quadrada do contador
  - Adicionar o ângulo áureo ao ângulo atual
  - Calcular a posição da semente, usando:
    
    \(posx = dist \times \cos{(ang)}\)
    
    \(posy = dist \times \sin{(ang)}\)
  - Acrescentar as posições nas listas de pontos
- Desenhar o gráfico usando pontos
Escreva um programa que implementa esse algoritmo, perguntando a quantidade de sementes desejada.

Para mais exemplos da razão áurea e dos números de Fibonacci, veja:
- Math is Fun: Fibonacci Numbers
- Connectivity Through Form: Sacred Geometry & the Golden Mean

Next Section - Repetição aninhada: Processamento de Imagens